Trigonometría y telecomunicaciones: la información vista desde el dominio de la frecuencia

Posted by noresnau on marzo 31, 2014 · 3 comentarios 

En la entrada de «La comunicación a través de ondas» habíamos explicado que el fenómeno físico de las ondas se puede aprovechar como vehículo para transportar información. Decíamos también que la información viaja en la forma de las ondas, poniendo como ejemplo las variaciones de la presión del aire que se producen al tocar una nota Re con un piano y una flauta. Volvemos a poner el dibujo:

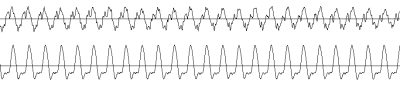
Una décima de segundo de un Re con piano (arriba) y con flauta (abajo).

Salta a la vista que son forma de onda claramente distintas, y es precisamente ahí donde está la información que nos permite diferenciar el sonido de los dos instrumentos. Nuestros sentidos de la vista y el oído, a fin de permitirnos reconocer cosas, llevan a cabo un procesamiento muy complejo de formas de onda, de oscilaciones eléctricas que se propagan a través de nervios que llegan al cerebro. Se trata de un procesamiento gestado a lo largo de millones de años de evolución, y que desde que nacemos tarda un tiempo considerable (meses o incluso años) en estar medianamente entrenado y funcional. De igual manera, los sistemas de telecomunicaciones se basan en manipular formas de onda para representar información y conseguir que viaje con éxito a través del medio que sea (un cable, el aire, el mar, etc). Para hacerlo con las prestaciones que tienen los sistemas modernos hemos tenido que desarrollar un aparato matemático fabuloso, cuyo máximo exponente es la herramienta que presentaremos hoy: la transformada de Fourier.

Si buscas por ahí encontrarás muchas explicaciones de la transformada de Fourier que parten de una de las fórmulas que ponemos a continuación, con integrales, exponenciales y otras cosas que a mucha gente le quitan las ganas de seguir leyendo. Nosotros intentaremos hacer ver que en esas fórmulas se esconden apenas un par de conceptos fáciles de entender. Empecemos, como casi siempre, por ver de dónde vienen las cosas.

Las fórmulas de la transformada de Fourier. ¡Tranquilos, que no cunda el pánico! (Crédito del dibujo de los niños: Prawny en FreeDigitalPhotos.net)

_

Lo que fueron aprendiendo los matemáticos de la Antigüedad.

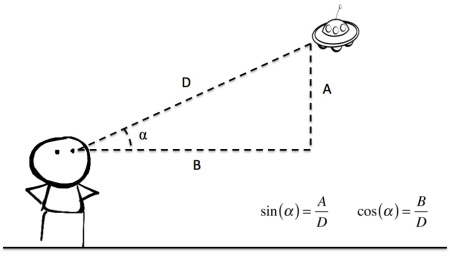
Las matemáticas de las telecomunicaciones tienen su origen en la trigonometría, una disciplina cuyo nombre significa, literalmente, «medir triángulos«. En ello se ocuparon sabios de todas las civilizaciones antiguas que tuvieron algún interés por la agricultura, la navegación e incluso la medida del tiempo, dada la importancia de determinar con un mínimo de precisión magnitudes tales como superficies de tierras cultivables, ángulos y distancias en el rumbo de los barcos, posiciones de los astros en el cielo, etc. Sumerios, babilonios y nubios pusieron el punto de partida hace más de 4000 años. Luego, empezando hace cosa de 22 siglos, griegos como Tales de Mileto, Euclides, Arquímedes, Pitágoras, Hiparco de Nicea o Apolonio de Pérgamo (nuestro favorito, un crack) dieron forma a los primeros teoremas y procedimientos de cálculo. Más adelante, los hindúes se hicieron eco de todo aquello e introdujeron, entre otras cosas, las nociones de seno y coseno en una especie de enciclopedia universal llamada Surya Siddhanta. Tampoco vayas a pensar que fueran dos definiciones espectaculares. Imagínate en la situación del siguiente dibujo, tumbado en el suelo y mirando hacia un objeto a cierta distancia de ti. Tu mirada define una línea hacia el objeto, y esa línea forma un ángulo ⍺ con la línea del suelo. Pues bien, el seno de ⍺ se define como el resultado de dividir la altura a la que se encuentra el objeto sobre la horizontal a la altura de tus ojos (A) entre la distancia a la que el objeto se encuentra de ti (D), mientras que el coseno de ⍺ se define como la división de lo que tendrías que caminar hasta llegar a estar justo debajo del objeto (B) entre, nuevamente, la distancia D.

Definiciones de seno y coseno sobre un triángulo rectángulo.

Ya en tiempos del gran matemático hindú Aryabhata, hacia el siglo V, los humanos teníamos perfectamente estudiadas las relaciones que se dan entre los 3 lados y los 3 ángulos de un triángulo. De este modo, conocidos 3 de esos datos, podíamos calcular con bastante precisión los otros 3 y alguna cosa más: la superficie del triángulo, las posiciones de sus 4 centros, etc. Posteriormente, los matemáticos del mundo árabe recopilaron, tradujeron y ampliaron esos conocimientos durante la Edad Media, destacando las aportaciones de al-Battānī y al-Tusi (otro crack del que hoy no se acuerda ni su p…ersa madre). Como siempre, los chinos llegaron al mismo conocimiento por su propia cuenta, de manos de fueras de serie como Shen Kuo (a quien ya nombramos en «Ciencia, tecnología y putadas tras la invención del telégrafo») y Guo Shoujing. Y, por supuesto, también hay evidencias sobradas de conocimientos de trigonometría en la América previa a la invasión europea, aunque en medio del expolio nadie se paró a hablar de matemáticas con los nativos.

«Sí, sí… sigue contando, Atahualpa, que ya me traen ahora la regla y el compás»

_

Lo que añadieron algunos matemáticos de la Edad Moderna

Por todas las vías que acabamos de comentar, hacia el siglo XV ya disponíamos de herramientas matemáticas con las que llevar a cabo medidas de longitudes y superficies de triángulos (y, por extensión, de cualquier polígono) con gran precisión, así como de sus circunferencias inscritas, circunscritas, tritangentes y demás. Esto de relacionar triángulos con circunferencias fue clave para el estudio científico de todo lo que tiene que ver con cosas que dan vueltas o que se repiten cíclicamente. Como ejemplo sencillo, en la visualización interactiva que enlazamos a continuación puedes ver un punto que se mueve sobre un círculo de radio 1, dibujando en cada momento un triángulo rectángulo con el centro de la rueda y la línea horizontal. Como la hipotenusa del triángulo mide 1 (igual que el radio del círculo), el seno y el coseno del ángulo que se forma en el centro del círculo nos devuelven directamente las medidas de los catetos. De este modo, podemos tener el punto móvil perfectamente localizado en cada momento… y quien habla de puntos que giran sobre círculos habla de ruedas, motores o satélites dando vueltas a la Tierra.

Haz clic sobre la imagen para abrir la visualización interactiva.

Con el Renacimiento europeo fueron ya muchos los que empezaron a hacer nuevas aportaciones a las matemáticas en general. Una aportación clave para otras muchas cosas que vendrían después la firmó el filósofo y matemático francés René Descartes: la geometría analítica. La idea –ya apuntada por Apolonio 1800 años antes, todo sea dicho– es definir líneas a través de fórmulas y representarlas en sistemas de coordenadas. Es justamente lo que hacemos en la animación de arriba para dibujar la circunferencia y el triángulo. Pero con el mismo planteamiento podemos representar, por ejemplo, cómo varía la longitud del cateto vertical a lo largo del tiempo: primero crece hacia arriba hasta medir 1, vuelve a decrecer, crece hacia abajo hasta medir 1 y vuelve a 0, para empezar otro ciclo. Resulta la curva que vemos abajo: la representación de la función seno, la onda más simple, lo que ya en «La comunicación a través de ondas» denominábamos una sinusoide.

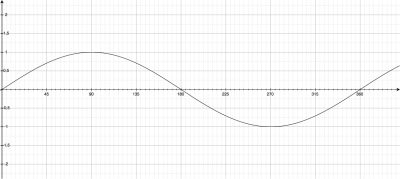
Representación gráfica del seno de un ángulo. Es una sinusoide de amplitud 1, frecuencia 1 y fase 0.

Haz clic sobre la imagen para abrir una visualización interactiva donde jugar un poco con los valores de amplitud, frecuencia y fase de una sinusoide.

Con las cosas así pintadas se abría un campo de investigación brutal en las matemáticas. Como lo de calcular áreas de polígonos regulares, círculos y elipses estaba ya muy visto, personajes como el inglés Brook Taylor, el suizo Leonhard Euler (pronunciado «/oiler/») y su amigo el holandés Daniel Bernoulli (de los Bernoulli de toda la vida, una saga de coquitos) buscaban el modo de expresar mediante fórmulas cualquier curva representada en unos ejes de coordenadas, para así tener una geometría capaz de hincarle el diente a lo que fuera. Llegamos así a 1822, cuando el francés Jean-Baptiste Fourier presentó una forma de descomponer cualquier función periódica en una suma de sinusoides. Concretamente, si una función repite un mismo dibujo con una cierta frecuencia, entonces se puede expresar como suma de una sinusoide de esa misma frecuencia, más otra del doble de frecuencia, más otra del triple, etc. Esas sinusoides son las denominadas componentes en frecuencia de la función original. La siguiente animación, adaptada de Wikipedia, ilustra estupendamente bien la idea (nuestro aplauso para el autor del original).

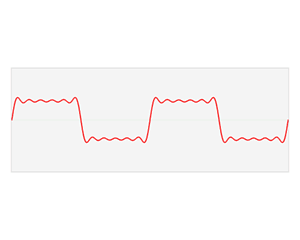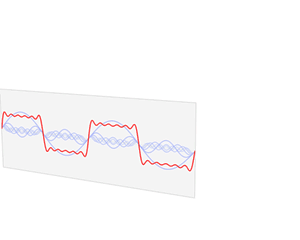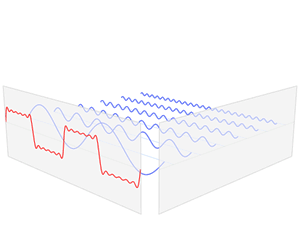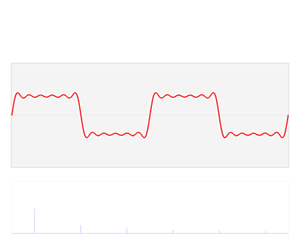
Desglose de una función periódica en 6 componentes, con la correspondiente representación en el dominio de la frecuencia. Las representaciones en tiempo y en frecuencia son sólo dos formas distintas de ver la misma cosa.

Las fórmulas de Fourier relacionan una función periódica en el dominio del tiempo (mostrada en rojo en la animación de arriba) con una serie de picos en el dominio de la frecuencia (mostrados en azul). Lo dicho: si la función repite un dibujo con frecuencia f, los picos se sitúan en las frecuencias f, 2f, 3f, etc. Y en cada pico hay dos números: uno indicando la amplitud de la componente correspondiente, y otro indicando su fase.

Fourier pronto generalizó sus fórmulas para poder describir cualquier función –no sólo las funciones periódicas– en el dominio de la frecuencia. En ese caso, ya no aparecen sólo un puñado de componentes en un determinado conjunto de valores de frecuencia, sino que pueden salir componentes en cualquier frecuencia: 0 Hz, 4.87 Hz, 10 KHz, 20.3333 MHz… Así pues, en general, una curva en el tiempo se corresponde con dos curvas en frecuencia: una indicando la amplitud de las sucesivas componentes y otra indicando sus fases. Esas representaciones reciben el nombre de espectro en frecuencia.

_

La transformada de Fourier y las telecomunicaciones

La transformada de Fourier es importante en la ingeniería de telecomunicaciones porque las formas de onda se pueden ver como funciones en un sistema de coordenadas. Por tanto, podemos manipular y analizar la información que va montada sobre las ondas tanto desde el dominio del tiempo como desde el dominio de la frecuencia. Y las posibilidades de éste último son muy amplias, como veremos a continuación.

Para empezar, volvamos a las formas de onda que poníamos al principio, de una misma nota tocada con flauta y con piano. Si quisiéramos fabricar un aparato capaz de reconocer la nota y el instrumento que se toca en un momento dado, sería bastante complicado diseñar un algoritmo que observase las variaciones de la presión sonora en el tiempo y las comparase con dibujos propios de cada nota y cada instrumento. En el dominio de la frecuencia, en cambio, la transformada de Fourier nos devolvería unos picos muy significativos. Ya sólo la frecuencia del primer pico nos indicaría la nota que está sonando, mientras que las amplitudes de los demás revelarían el instrumento utilizado. Viendo los espectros correspondientes a ambas formas de onda (mira abajo) salta a la vista que la caja de resonancia del piano genera muchos picos, cuya amplitud baja suavemente a medida que aumenta la frecuencia. En cambio, la flauta exhibe unos pocos picos importantes (hasta 3 KHz, más o menos) y poco más. Si en vez de un Re hubiéramos hecho sonar cualquier otra nota, se observaría algo muy parecido. Por tanto, el dominio de la frecuencia nos ofrece un método fácil y directo para distinguir notas e instrumentos. Afinando un poco más y complementando con otras cosas, podríamos hablar de transcripción automática de partituras, reconocimiento de voz, etc.

Amplitudes de las componentes en frecuencia de un Re tocado con piano.

Amplitudes de las componentes en frecuencia de un Re tocado con flauta.

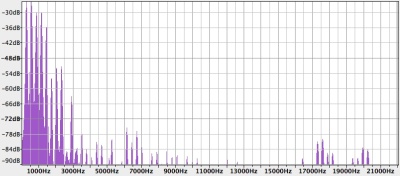
Por otra parte, pensemos eso de que «cualquier forma de onda, por compleja que sea, se puede expresar como combinación de múltiples sinusoides de diferentes frecuencias, amplitudes y fases«. Obviamente, cuantas más sinusoides se combinen, más información transportará la onda resultante. Así pues, observando lo que haya en el dominio de la frecuencia nos podremos hacer una idea muy clara de la cantidad de información que transporta una onda. Por ejemplo, a continuación mostramos las amplitudes de las componentes en frecuencia de dos fragmentos de audio de la misma duración (más o menos): uno de voz y otro de música. Salta a la vista que la música se extiende por un rango de frecuencias mucho más amplio, con componentes de hasta 20 KHz donde la voz no pasa de 6 KHz (vale que Eugenio era un caso extremo de voz grave, pero sirve como ejemplo). Por eso, a pesar de lo pobre que es la poesía de Pitbull, el fragmento de música contiene más información. Luego no es de extrañar, como comentábamos en «Las guerras de la radio», que los primeros sistemas de radio se utilizaran para difusión de voz, mientras que la difusión de música se hizo esperar hasta que llegaron una serie de avances técnicos: no era trivial construir aparatos que funcionasen bien en un margen de frecuencias el doble de grande. A todo esto, hay que decir que en el dominio del tiempo es muy difícil apreciar si una cosa contiene más información que la otra, por lo que es seguro que la tecnología no habría evolucionado como lo hizo si no llega a ser por el bueno de Fourier.

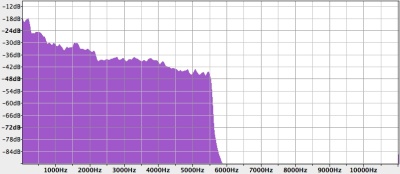
Espectro en frecuencia de un chiste de Eugenio. ¡Se te echa de menos, maestro!

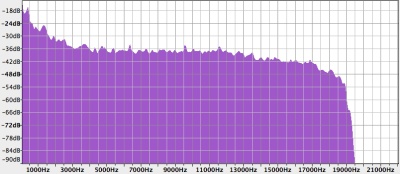
Espectro de un fragmento de «Yo no quiero agua, yo quiero bebida». Fíjate que el eje horizontal va hasta 21 KHz, y no hasta 11 KHz como la imagen de arriba.

Finalmente, hay que destacar que la frecuencia no es un concepto matemático abstracto, sino algo con una realidad física detrás. Muchísimas cosas en la naturaleza responden de manera diferente a estímulos de distintas frecuencias. Sin ir más lejos, ya hemos explicado aquí que nuestro oído no responde por igual a sonidos de todas las frecuencias, sino que percibe unas frecuencias mejor que otras y sólo dentro de un rango determinado. Igualmente, ya sabes que nuestra visión sólo percibe ondas de frecuencias por encima de los infrarrojos y por debajo de los ultravioleta (si no lo sabes, pulsa aquí). Ambos fenómenos pueden verse como el resultado de una operación de filtrado que tiene lugar en los oídos y los ojos, por la cual unas componentes de las ondas que les llegan se transmiten intactas a los nervios correspondientes, mientras que otras se atenúan y/o sufren cambios de fase y otras desaparecen por completo. En lo tocante a las telecomunicaciones, hay que decir que la gran mayoría de los medios por los que enviamos ondas actúan como filtros y sólo transmiten ondas dentro de un cierto rango de frecuencias. Debido a los cambios de amplitud y fase, las formas de onda que llegan a los receptores rara vez son una copia exacta de las que salieron de los emisores. Y ya no hablemos del ruido, que complica todavía más la labor de recuperar la información montada sobre las ondas. A todo esto, aunque ya hablaremos de ello más adelante, la primera medida para hacer frente al ruido siempre es… ¿sabes qué? Sí, un filtro, concretamente uno que elimine todas las componentes de frecuencias donde sabemos que no hay nada de la información que nos interesa. Podríamos seguir poniendo ejemplos, pero el caso es que, nuevamente, la transformada de Fourier ha sido clave para llegar a entender todas estas cosas.

_

En resumen

Hoy hemos presentado una herramienta básica no sólo en la ingeniería de telecomunicaciones, sino también en otras muchas ramas de la ingeniería y de la física. El estudio que habilita la transformada de Fourier en el dominio de la frecuencia es fundamental para comprender muchos fenómenos de la naturaleza y sacarles partido en nuestra tecnología. Métete en la cabeza eso de que cualquier forma de onda se puede descomponer como suma de sinusoides de distintas amplitudes, frecuencias y fases, que se pueden manipular de manera casi quirúrgica para meter información en las ondas, para extraerla, para adaptarla a las condiciones de transmisión que ofrece cada medio, para eliminar ruido y corregir distorsiones, … y muchas cosas más. Una virguería salida de la mente de un matemático del siglo XIX que no habría sido posible sin las contribuciones de decenas de entusiastas de la geometría ya desde poco después de la invención del taparrabos.

Fuck yeah! (Créditos del troglodita: Grant Cochrane en FreeDigitalPhotos.net)

 

Archivado en conceptos, matemáticas, ondas · Tagged with Divulgación científica, Espectros en frecuencia, Jean-Baptiste Fourier, Transformada de Fourier, Trigonometría